
Autor: 23.02.2024
Jak działa średnia ważona (prosty wzór)
Niemal każdy z nas kojarzy czym jest średnia: sumujemy wartości i dzielimy wynik przez ilość tych wartości. Więcej problemów może sprawić tzw. średnia ważona. Używa się jej często, chociażby w edukacji, ponieważ pozwala przypisać różne wagi, różnym ocenom. Dlatego przygotowaliśmy ten artykuł, który wyjaśni Ci sposób obliczania średniej ważonej. Zaczynamy!
Definicja średniej ważonej
Średnia ważona to rodzaj średniej, w której każdy element zbioru danych ma przypisaną wagę. Ta waga określa, jak bardzo dany element wpływa na ogólną średnią. Wartości bardziej ważne mają większy wpływ na wynik niż wartości mniej ważne.
Można sobie wyobrazić przeróżne zastosowania takiej średniej. Bardzo często używamy jej w edukacji - dzięki niej możemy przypisać ocenom z różnych przedmiotów, różne wagi.
Jak obliczyć średnią ważoną ocen
Załóżmy, że masz dane dotyczące wyników ucznia, a także informacje o tym, która ocena jest bardziej istotna, a która mniej. Spójrz na poniższą tabelkę:
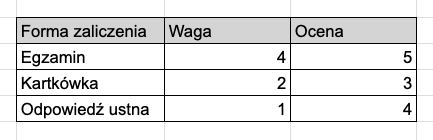
Egzamin jest najbardziej kluczowy, ponieważ posiada najwyższą wagę czyli 4. Odpowiedź ustna nie jest aż tak istotna, dlatego zdecydowaliśmy przydzielić jej wagę o wartości 1.
Najpiew wyjaśnijmy sobie kluczowe elementy.
o1 = ocena 1, o2 = ocena 2, o3 = ocena 3
w1 = waga 1, w2 = waga 2, w3 = waga 3
Czyli mamy oceny od o1 do o3, oraz wagi od w1 do w3. Teraz podstawmy te wartości do wzoru na obliczenie średniej ważonej:
średnia ważona = (o1 * w1) + (o2 * w2) + (o3 * w3) / (w1 + w2 + w3)
Musimy zsumować iloczyny wag oraz ocen, i następnie podzielić wynik przez sumę wag. Spróbujemy więc wykonać te operacje krok po kroku:
średnia ważona = (5 * 4) + (3 * 2) + (4 * 1) / (4 + 2 + 1)
średnia ważona = 20 + 6 + 4 / 7
średnia ważona = 30 / 7
średnia ważona = 4.29 (wynik przybliżony)
Średnia ważona dla ucznia wynosi około 4.29, uwzględniając różne wagi ocen. Dzięki temu mamy średnią, która uwzględnia różne znaczenie ocen - jak pewnie pamiętasz ocena z egzamiu jest ważniejsza niż ocena z kartkówki, a ta z kolei jest ważniejsza niż ocena z odpowiedzi ustnej.
Zastosowania średniej ważonej
Przykład, który pokazaliśmy to chyba najbardziej powszechne zastosowanie średniej ważonej. Ale ma ona wiele innych zastosowań.
W analizach finansowych, poszczególne wskaźniki finansowe mogą być obliczane z użyciem średnich ważonych, aby uwzględnić różne wagi różnych pozycji w danych finansowych.
W badaniach naukowych, gdy różne próby mają różne znaczenia lub wpływ, stosuje się średnie ważone do obliczania wyników analiz.
To tylko wybrane przykłady użycia - można by ich śmiało znaleźć znaczniej więcej.
Podsumowanie
Średniej ważonej używamy tam, gdzie trzeba uwzględnić różne wagi, dla różnych wartości. To jedna z fundamentalnych koncepcji statystycznych.
Jeśli chcesz dowiedzieć się więcej na temat najważniejszych pojęć używanych w statystyce to zapraszamy na kurs Podstawy statystyki dla początkujących. Dzięki niemu szybko zrozumiesz kluczowe pojęcia używane w statystyce, nauczysz się wyliczać najważniejsze miary statystyczne oraz dowiesz się jak prawidłowo intepretować wyniki.

















