Autor: Codenga 19.10.2023

W tym artykule wyjaśnimy czym są kombinacje oraz permutacje. Te dwa pojęcia stanowią ważną część dziedziny znanej jako kombinatoryka. Każde z pojęć objaśnimy za pomocą prostego języka, pokażemy także kilka przykładów. Artykuł przeznaczony jest dla czytelników, którzy nie mieli wcześniej do czynienia z tym tematem, i chcą zrozumieć sens pojęcia kombinacji oraz permutacji. Do zrozumienia treści poruszanych w artykule potrzebna jest umiejętność obliczania silni.

Kombinacje - co to jest

Kombinacja to pojęcie w kombinatoryce, które opisuje różne zestawy elementów wybranych z danego zbioru, ale bez uwzględniania kolejności, w jakiej te elementy są ułożone.

Oto wzór matematyczny na kombinację:

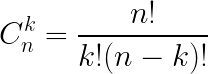
Gdzie:

• n to liczba dostępnych elementów,
• k to liczba miejsc lub pozycji do ustawienia elementów.

Przykład

Jeśli mamy zbiór { A, B, C, D } i chcemy utworzyć 2-elementową kombinację, możemy to zrobić na kilka sposobów:

• AB
• AC
• AD
• BC
• BD
• CD

Wszystkie te kombinacje nie uwzględniają kolejności elementów i stanowią po prostu różne zestawy wybranych elementów ze zbioru.

Postarajmy się upewnić, czy faktycznie ze zbioru 4-elementowego możemy uzyskać 6 kombinacji par. Zastosujemy w tym celu pokazy przed chwilą wzór.

Zbiór posiada 4 elementy (n = 4). Chcemy wygenerować kombinację 2-elementowych par, czyli k = 2. Podstawmy nasze dane do wzoru:

n! / (k!(n-k)!) = 4! / (2!(4 - 2)! = 24 / (2 * 2!) = 24 / (2 * 2) = 24 / 4 = 6

Wszystko się zgadza. Nasze przewidywania zostały potwierdzone obliczeniami. Tak więc wygląda podstawowe pojęcia kombinacji. To nic innego jak pewien zestaw elementów ze zbioru, który nie uwzględnia pozycji elementów (inaczej: pozycje elementów nie mają znaczenia).

Permutacje - co to jest

Permutacja to pojęcie z matematyki i kombinatoryki, które opisuje różne sposoby ustawienia lub układania elementów w określonej kolejności. Można sobie to wyobrazić jako różne aranżacje lub kolejności, w jakich można umieścić dane elementy.

Przykład

Załóżmy, że mamy trzy różne kule bilardowe opisane jako A, B i C. Permutacja tych elementów oznacza różne sposoby ustawienia elementów A, B i C. Oto przykład permutacji naszych kulek:

• ABC
• ACB
• BAC
• BCA
• CAB
• CBA

Nasze 3 kule możemy ustawić w 6 różnych konfiguracjach. Skąd wiemy, że możemy je ułożyć na maksymalnie 6 sposobów? W tej sytuacji pomocna będzie silnia.

Wystarczy wyznaczyć silnię z wszystkich elementów zbioru (mamy 3 elementy: A, B i C), czyli 3! = 3 * 2 * 1 = 6 (3 kulki możemy ułożyć na 6 różnych sposobów).

Tutaj działa bardzo prosta zasada - chcesz wiedzieć ile jest możliwych permutacji w danym zbiorze? Po prostu wyznacz silnię ze wszystkich elementów zbioru.

Podsumowanie i dalsze kroki

Mamy nadzieję, że po lekturze tego artykułu wiesz już czym są kombinacje oraz permutacje. Stanowią one bardzo istotną cześć tzw. kombinatoryki. Jeśli chcesz dowiedzieć się więcej na temat kombinatoryki oraz opanować podstawy rachunku prawdopodobieństwa, to zapraszamy na kurs Codenga Wprowadzenie do kombinatoryki oraz prawdopodobieństwa.

Poznaj fascynujący świat kombinatoryki oraz prawdopodobieństwa. Opanuj najważniejsze pojęcia i wykonaj wiele praktycznych zadań.

Dowiedz się więcej