Autor: Codenga 14.02.2024

Statystyka to klucz do zrozumienia świata, który nas otacza. Dzięki niej wiemy jak interpretować dane oraz informacje. Ten artykuł wyjaśnia prostym językiem osiem podstawowych pojęć oraz miar używanych w statystyce. Stanowią one swoisty fundament, który musisz poznać na samym początku.

Średnia arytmetyczna

Średnia arytmetyczna to jedno z najprostszych pojęć statystycznych. Po prostu suma wszystkich wartości w zbiorze podzielona przez liczbę tych wartości. Na przykład, jeśli mamy zbiór liczb: {2, 4, 6, 8}, średnia arytmetyczna wynosi (2 + 4 + 6 + 8) / 4 = 5.

Są też inne, bardziej złożone odmiany średniej - na przykład średnia ważona.

Mediana

Mediana to wartość, która dzieli zbiór danych na dwie równe części, gdy są one uporządkowane w kolejności rosnącej lub malejącej. To oznacza, że połowa wartości jest większa, a połowa mniejsza od mediany. Na przykład, dla zbioru liczb {3, 5, 7, 9, 11}, mediana wynosi 7.

Jeśli z kolei ilość elementów w zbiorze jest parzysta, to medianą jest średnia arytmetyczna dwóch środkowych elementów. Przykład:

Rozważmy zestaw danych dotyczący wieku sześciu osób: 10, 15, 18, 20, 22, 25.

• Uporządkujmy dane rosnąco: 10, 15, 18, 20, 22, 25.
• Ponieważ liczba elementów jest parzysta, mediana będzie średnią arytmetyczną dwóch środkowych elementów. W tym przypadku są to 18 i 20.
• Obliczmy średnią arytmetyczną: (18 + 20) / 2 = 38 / 2 = 19.
• Mediana dla tego zestawu danych wynosi 19.

Odchylenie standardowe

Odchylenie standardowe to miara rozproszenia danych wokół średniej. Im większe odchylenie standardowe, tym bardziej dane różnią się od średniej. Jest to przydatne narzędzie do określenia, jak bardzo dane są "rozproszone" wokół średniej.

Percentyl

Percentyl to punkt, poniżej którego znajduje się określony procent obserwacji w zbiorze danych. Jest to przydatne pojęcie do porównywania wartości w stosunku do całego zbioru danych. Na przykład, 25. percentyl oznacza, że ​​25% obserwacji w zbiorze znajduje się poniżej tej wartości.

Histogram

Histogram to rodzaj wykresu, który przedstawia rozkład danych na osiach, gdzie jeden z nich reprezentuje wartości, a drugi liczbę wystąpień tych wartości. Jest to przydatne narzędzie do wizualizacji rozkładu danych i identyfikacji wzorców. Oto przykład histogramu:

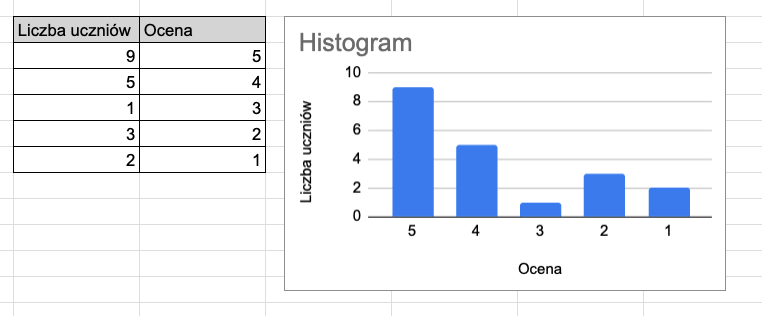
Na powyższym histogramie zaprezentowano rozkład ocen. Od razu widać, że najczęściej wystąpiła ocena 5. Z kolei najrzadziej występuje ocena 3 (najniższy słupek). Na drugim miejscu, pod względem popularności, jest ocena 4.

Rozkład normalny

Rozkład normalny jest to rodzaj rozkładu statystycznego, w którym większość danych skupia się wokół średniej, a wartości odchylające się od średniej maleją symetrycznie w obie strony. Jest to często spotykany rozkład w naturze i w wielu dziedzinach nauki.

Testy statystyczne

Testy statystyczne są to narzędzia używane do analizy danych i sprawdzania hipotez statystycznych. Są one stosowane do określenia, czy wyniki badania są istotne statystycznie i czy różnice między grupami są rzeczywiste czy przypadkowe.

Próba losowa

Próba losowa jest to sposób wybierania próbek z populacji. Ma on zapewnić, że każdy element populacji ma równą szansę być wybranym do analizy. Jest to kluczowy aspekt wielu badań statystycznych i jest niezbędny, aby uzyskać reprezentatywne wyniki.

Przykład:

Załóżmy, że jesteś dyrektorem szkoły podstawowej i chcesz ocenić średnią ocen uczniów w swojej szkole. Twoja szkoła ma 500 uczniów.

Co to takiego populacja? Zbiór wszystkich 500 uczniów w twojej szkole stanowi populację. A to oznacza, że chcielibyśmy poznać średnią ocen wszystkich uczniów w całej szkole.

Co to takiego próba? Ze względów czasowych i zasobowych nie jesteśmy w stanie ocenić każdego ucznia. Dlatego losowo wybieramy 50 uczniów ze szkoły (przy zachowaniu różnorodności, na przykład wybieramy 5 uczniów z każdej klasy). Te 50 uczniów stanowi próbę.

Podsumowanie

Zrozumienie tych podstawowych pojęć statystycznych może być kluczowe dla lepszego zrozumienia danych i informacji, które nas otaczają. Mamy nadzieję, że ten prosty przewodnik pomoże Ci zrozumieć podstawy tej niezwykle ważnej dziedziny.